1 тип задач
| Действия над комплексными числами: умножение, деление, возведение в степень и извлечение корня из комплексных чисел.
| Действия над комплексными числами
| 1. Сложение, вычитание и умножение комплексных чисел делается по следующим правилам: k=1∑k=n(ak+ibk) = k=1∑k=n ak + ik=1∑k=n bk (a1 + ib1) - (a2+ib2) = (a1-a2) + i(b1 - b2) (a1 + ib1)(a2 + ib2) = (a1a2 - b1b2) + i(a1b2 + a2b1) 2. Возведение комплексных чисел в степень с целым положительным показателем степени производится по формуле бинома Ньютона, причем степени i (мнимой единицы) определяются следующими формулами: i4k+1=i; i4k+2=i2=-1; i4k+3=i3=-i; i4k+1=i4=1 (i=1, 2,...). Так, (a+ib)2 = a2 + 2aib + (ib)2 = a2 + 2iab - b2 = (a2 - b2) + 2aib (a+ib)3 = a3+3ia2b - 3ab2 - ib3 = (a3 - 3ab2) + i(3a2b - b3) и т.д. 3. При делении комплексных чисел числитель и знаменатель дроби умножаются на комплексное число, сопряженное со знаменателем: (a1 + ib1)/(a2 + ib2) = [(a1+ib1)(a2-ib2]/[(a2+ib2)(a2-ib2] = [(a1a2 + b1b2) + i(a2b1 - a1b2)]/[a22 + b22] = 4. Извлечение корня из комплексного числа. Для того, чтобы извлечь корень n-й степени (n - целое, положительное) из комплексного числа z=x+iy, надо прежде всего представить его в показательной форме Здесь r=|z|=√(x2+y2) (модуль комплексного числа). φ = argz (главное значение аргумента комплексного числа, т.е. то значение Argz, которое удовлетворяет неравенству -П < φ < П). Угол φ определяется либо равенствами cos φ = x/r = x/[√(x2 + y2)]; sin φ = y/r = y/[√(x2 + y2)], либо формулой φ = arctg(y/x) + C, где C=0 при x>0; С=П при x < 0 y>0; С=-П при x < 0, y < 0. Для отыскания всех значений n√(z) надо воспользоваться формулой n√ = n√ (reiφ) = n√ (r ei(φ+2kП) = n√ (r)*ei(φ+2kП)/n, где k=0,1,2,...,n-1. Таким образом, u=n√(z) = ρeiΨ, где ρ = n(r) (здесь корень понимается в арифметическом смысле), а Ψ = φ/n + 2kП/n (k=0,1,2,...,n-1). Так находятся все n различных значений искомого корня. Таким образом, все n различных значений корня n-й степени из некоторого комплексного числа z изображаются на плоскости комплексного переменного точками, лежащими на одной и той же окрудности с радиусом ρ = n√(|z|) и центром в нулевой точке. Поскольку же разности аргументов любой пары соседних (по окружности) из этих точек постоянны и равны 2П/n, эти точки являются вершинами некоторого правильного n-угольника, вписанного в эту окружность. Пример.
| Даны числа z1 = √3 - i; z2 = -2+2i√3. Найти
Найти (z1/
z1/ (z1/ Найти: 3√[(
|
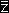 1z2;
1z2;