| Задача 2.1
Построить графически распределение модулей вектора индукции магнитного поля B, напряженности магнитного поля H, а также вектора намагниченности J в зависисмости от r в интервале от R до R0. Определить поверхностный ток намагничивания i на внутренней и внешней поверхностях трубки на единицу длины; распределение плотности токов намагничивания jn в объеме магнетика. Функция µ = f(r) для четных вариантов имеет вид: Функция µ = f(r) для нечетных вариантов имеет вид:
Задача 2.2
|
Построить графически распределение модулей вектора индукции B и напряженности H магнитного поля, а также вектора намагниченности J в зависимости от r в интервале от R до R0. Определить поверхностный ток намагничивания i на внутренней и внешней поверхностях магнетика на единицу длины, распределение плотности токов намагничивания jH в объеме магнетика. Определить индуктивность единицы длины кабеля. Функция µ = f(r) для четных вариантов имеет вид: Функция µ = f(r) для нечетных вариантов имеет вид:
Задача 2.3
|
Построить графически распределение индукции B и напряженности H магнитного поля, а также вектора намагниченности J в зависимости от y в интервале значений от 0 до d. Определить поверхностный ток намагничивания i на верхней и нижней поверхностях магнетика на единицу длины; распределение плотности токов намагничивания jН в объеме магнетика. Определить индуктивность единицы длины этой двухполосной линии. Функция µ = f(y) для четных вариантов имеет вид: Функция µ = f(y) для нечетных вариантов имеет вид:
Для всех вариантов.
| По результатам проведенных вычислений построить графически зависимости B(r)/B(R), H(r)/H(R) в интервале значений R от R до R0 для задач 2.1 и 2.2, а также зависимости B(y)/B(0), H(y)/H(0) в интервале значений y от 0 до d для задачи 2.3. Все зависимости изобразить на одном графике. Решение задачи 2.1.
| Для контура радиуса r запишем теорему о циркуляции вектора напряженности H магнитного поля: ∫Hd(I) = 2ПrH = jП(r2 - R2), откуда H = j(r2 - R2)/2r тогда: B = µµ0H = µµ0j(r2 - R02)/2r = (R0n + rn)µ0j(r2 - R02)/R0n2r J = xH = (µ - 1)j(r2 - R02)/2r = rnj(r2 - R2)/R0n2r Поверхностная плотность тока намагничивания i численно равна касательной составляющей вектора намагничивания J к поверхности если поверхность является поверхностью раздела магнетика и вакуума. i(R) = 0, i(R0) = j(R02 - R2)/2R0 Объемную плотность тока намагничивания jH можно найти используя теорему о циркуляции вектора J: ∫Jd(I) = IH где IH - суммарный ток намагничивания, пронизывающий данный контур. В качестве контура выберем две окружности r и r+dr. Циркуляция по окружности радиуса r равна 2rПJ(r), тогда для контура можно записать: d(2ПrJ) = jH(2Пrd(r)) Откуда: jH = (j/2R0nr)(d/dr(rn(r2-R2))) = (j/2R0n)((n+2)rn - nR2rn-2) Основные формулы магнитостатики
| Связь между векторами B,H,J: B = µµ0H, J = (µ - 1)H Теорема о циркуляции вектора нпряженности магнитного поля H: ∫LHdl = I, где I - ток, пронизывающий данный замкнутый контур. Теорема о циркуляции вектора намагниченности J: ∫LJdl = Iн, где Iн = ∫jнdS - ток намагниченности пронизывающий данный замкнутый контур L. Теорема Гаусса для вектора индукции магнитного поля: ∫BdS = 0 Индуктивность: L = (1/I2)∫V(BH)dV или L = Ф/I, где Ф = ∫SBdS - поток вектора магнитной индукции через поверхность S, ограничивающую данный контур. |
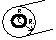Проводник с током плотности j равномерно распределенным по его поперечному сечению имеет форму трубки, внешний и внутренний радиусы которой равны R0 и R соответственно. Магнитная проницаемость меняется по закону µ = f(r).
По коаксиальному кабелю, радиусы внешнего и внутреннего проводника которого равныR0 и R соответственно, протекает ток I. Пространство между проводниками заполнено магнетиком, магнитная проницаемость которого меняется по закону µ = f(r).
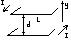Два плоских проводника с токами I, текущими в противоположных направлениях, разделены слоем магнетика толщины d. Ширина проводников равна L (L>>d). Магнитная проницаемость µ магнетика меняется в направлении оси у по закону µ = f(y).
